|
|
|
|
|
|
|
|
|
|
|
|
|
|
Newton I. törvénye
Definíció:
A testeknek az a tulajdonsága, hogy mozgásállapotuk csak erő hatására változik meg, ez a testek tehetetlensége.
Newton első törvénye a TEHETETLENSÉG TÖRVÉNYE
Minden test megmarad a nyugalom vagy az egyenes vonalú egyenletes mozgás állapotában mindaddig, amíg valamilyen erőhatás ennek elhagyására nem kényszeríti.
! Az olyan vonatkoztatási rendszereket, amelyekben teljesül a tehetetlenség törvénye, inerciarendszereknek nevezzük.
(A Newton-törvények csak inerciarendszerekben érvényesek)
Newton II. törvénye
Newton második törvénye a DINAMIKA ALAPTÖRVÉNYE
A tömegpontot a fellépő erő a saját irányába gyorsítja, a létrejövő gyorsulás pedig egyenesen arányos az erővel.
F ~ a
A testre ható erő és a gyorsulás hányadosát a test tehetetlen tömegének nevezzük, jele m.
F = m * a
Az erő mértékegysége a tömeg és a gyorsulás egységének szorzata,
1 kg * 1 m/s2 = 1 N (newton)
! 1N az az erő, amely az 1 kg tömegű testet 1 m/s2 gyorsulással mozgatja.
A dinamika alapegyenlete
- A testre ható erők egymástól függetlenül fejtik ki hatásukat.
- A tömegpontra ható erők eredője egyenlő a test tömegének és gyorsulásának szorzatával. A gyorsulás az eredő erő irányába mutat.
Ez a tétel a DINAMIKA ALAPEGYENLETE.
Hasonlóképpen egy testre a gravítációs mező által gyakorolt gravitációs erő, például a test súlya a föld gravitációs mezőben, arányos a test tömegével:
G=m*g
(A szimuláció megtekintéséhez katincson a képre)
A g gravitációs gyorsulás a föld középpontja felé irányul , éppen úgy, mint a test súlya, értéke: g~9,8 m/s˛ (függ a tenger szintjétől számított magasságtól és a földrajzi szélességtől).
Newton III. törvénye
Newton harmadik törvénye A HATÁS-ELLENHATÁS TÖRVÉNYE
Ha az egyik test erőt fejt ki a másikra, a másik is erőt fejt ki az előzőre, tehát az erők mindig párosával lépnek fel. Ezek az erők egyenlő nagyságúak és ellentétes irányúak. Az egyik a hatás, a másik a visszahatás.Azt, hogy a két erő közül melyiket tekintjük hatásnak és melyiket visszahatásnak, az csak attól függ, hogy melyik testet vesszük elsőnek és melyiket másodiknak.
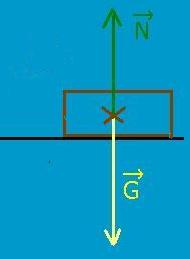
A föld és egy test esetében ahatást a test gyakorolja a földre, mig a föld a testre a visszahatást. Ebből következik, hogy
G = N
Egy másik példa a csigán átvetett szál két végére felfogatott két test. Ebben az esetben a csiga mindkét felén lógo testek hatnak a szálra, és a szál visszahat rájuk. Tökéletes csiga és nyujthatatlan szál esetében a testek elmozdulnak, és azonos gyorsulással mozognak, csak ellentétes irányba. Az egyik test felfele, mig a másik lefele. Az irányt a nagyobbik test súlyának irányítása adja meg.
A fentiekből következik, hogy ha a szál visszaható erejét T-vel jelöljűk, és a súlyokat G1 illetve G2 - vel és G1>G2:
G1-T=m1*a
T-G2=m2*a
(A szimuláció megtekintéséhez katincson a képre)
Súrlódási erők
A súrlódás erő a mozgás síkjában hat, és a test sebességevel ellentétes irányítású. Az érintkezési sÍkban két súrlódási erő hat, a hatás- ellenhatásnak megfelelően, amelyek modulusa egyenlő és ellentétes irányításúak, egyik a testre, a másik a síkra hat.
Ha egy test egy másik testen elmozdul (súszik), az érintkezési felület síkjában súrlódási erő lép fel, a két test közötti viszonylagos sebességgel ellentétesen.
Ha N jelöli az érintkezési felületre ható merőleges nyomóerőt és µ az arányossági tényező, írhatjuk, hogy :
Fs=µN ahol N=G
A µ arányossági tényezőt súrlódási együtthatónak nevezzük.
A fentie összegzésével bemutatunk egy pár, gyakrabban előfordúló mechanikai mozgást.
1. Ilyen például a test mozgása a vízszintesen, ahol a testre ható erők az F- húzóerő, Fs- súrlódási erő, G- a test súlya, és ennek ellenszegűlő erő a N- a felszin visszaható ereje. Ezen erők ismeretében felirhatjuk a következő egyenletett.
F-Fs=m*a; G-N=0;
ahol tudjuk, hogy: Fs=µ*m;
(A szimuláció megtekintéséhez katincson a képre)
2. Egy másik példa, amikor a test a lejtőn mozog saját súlya és egy F - erő hatására. Ebben az esetben a G -súlyot felbontjuk (lásd a vektorok összeadását), igy a testet nem egész G súly, hanem annak (Gt) tangemciálisa gyorsítja az F - erővel eggyűt.A felszinre hetó erő nem lesz más mint a Gn (normál).
Most pedig felírjuk az egyenleteket is :
F+Gt-Fs=m*a; Gn-N=0;
(A szimuláció megtekintéséhez katincson a képre)
3.A fenti példa ellentetje, amikor a test felfele mozog egy F-erő hatására. Ebben az esetben megváltozik a surlódás irányítása is.Ebben az esetben az egyenlet:
F-Gt-Fs=m*a; Gn-N=0;
(A szimuláció megtekintéséhez katincson a képre)