|
Műveletek vektorokkal
A vektorokkal való föbb műveletek: összeadás, kivonás.
A következőben ezeket a műveleteket tanulmányozzuk.
|
Műveletek vektorokkal
A vektorokkal való föbb műveletek: összeadás, kivonás.
A következőben ezeket a műveleteket tanulmányozzuk.
A vektorok összeadása. A vektorok összeadása geometriai úton történik az ún. paralerogramma szabály segítségével.
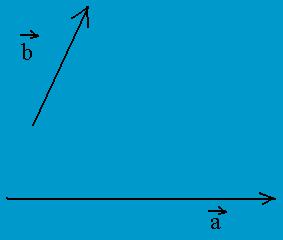
Két, például az a és b vektort úgy adunk össze, hogy az egyik vektor kezdőpontját a másik csúcspontjába rajzoljuk, majd összekötjük az első vektor kezdőpontját a második csúcspontjával. Ez a záróvektor adja meg a két vektor összegét.
Ha az a vektor támpontjából egy, a b vektorral párhuzamos vektort húzunk, és ezekre egy paralelogrammát szerkesztünk, ennek az átloja adja meg két vektor összegét. Innen ered a palalelogramma szabály:
Két vektor összegét annak a paralelogrammának az átlója adja meg, amelynek oldalait a közös támpontú vektorok alkotják
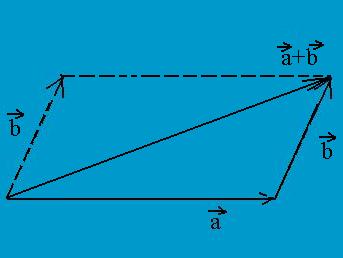
Az összegvektor modulusa az általánosított Pitagorasz- tétel segítségével számítható ki:
s˛=a˛+b˛+2aˇbˇcosα
ahol α az a és b vektorok álltal bezátr szög.
A vektorok kivonása:Ha valamely vektor modulusa nullára csökken, akkor a vektor nullvektornak tekintjük, és 0-val jelöljük, akárcsak a nulla számot. A zérusvektor iránya határozatlan. Ha például több vektor összeadásánál a sokszög bezárul, akkor az adott vektorok összege nulla. Hasonlóképpen, ha két egyenlő nagyságú és irányú, de ellentétes irányításu vektort adunk össze, ugyancsak nullvektort kapunk. Ebből következik, hogy bármelyik nullától külömböző a vektornak megfelel egy ellentétes vektor a1=-a, amelynek ugyanakkora a modulusa, ugyanaz az iránya, azonban ellentétes az irányítása. Ha ezeket a vektorokat összegezzük, eredményül zérusvektort kapunk.
Most már meghatározhatjuk a vektorok kivonását:
ha az a vektorból ki kell vonni a b vektort, ez azt jelenti, hogz az a vektorhoz hozzá kell adni az ellentétes -b vektort:
a - b = a + (-b)
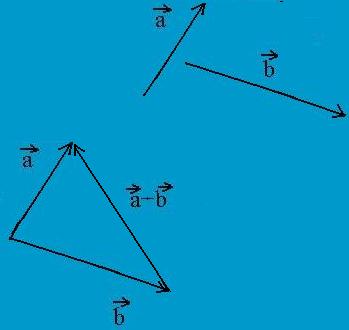
Két vektor külömbségét úgy kapjuk meg, hogz mindkettőt ugyanabban a kezdőpontban rajzoljuk fel, majd egyesítjük a csúcsaikat úgy, hogy a nyíl a kisebbítendő vektor felé mutasson.